Monitoring respiratory mechanics in mechanically ventilated patients

Article

Author: Dr. med. Jean-Michel Arnal, Senior Intensivist, Hopital Sainte Musse, Toulon, France

Date of first publication: 17.06.2020

Last change: 17.06.2020

First published 25.04.2018: Resistance cm2/l/s changed to cm2/(l/s)

The term respiratory mechanics describes the mechanical properties of the respiratory system that is inflated during mechanical ventilation. Monitoring respiratory mechanics is useful for diagnosing the lung condition, assessing the evolution and severity of the lung impairment, and adjusting ventilator settings.

Monitoring respiratory mechanics in mechanically ventilated patients

Take-away messages

Take-away messages

Monitoring respiratory mechanics helps to assess and diagnose the lung condition and impairment, and adjust the ventilator settings.
The two main products of respiratory mechanics are compliance and resistance.
The time constant describes the speed of the change in volume after a step change in pressure and is the product of resistance and compliance, measured at inspiration or expiration.
The expiratory time constant is very useful for assessing the overall respiratory mechanics and the changes in them.
A short expiratory time constant indicates a decrease in compliance, while a long one indicates increased resistance.

Measurement of respiratory mechanics

The main properties of respiratory mechanics are compliance and resistance. Other properties, such as inertia and viscoelasticity, do not play a significant role in conventional mechanical ventilation and can therefore be discounted. Respiratory mechanics are usually measured using airway pressure and flow; therefore, the assessment of the respiratory system’s properties includes the endotracheal tube. However, more precise measurements may be obtained in particular cases by using tracheal pressure at the carina, which enables us to separate the endotracheal tube and airway resistance. Esophageal pressure allows us to partition the chest wall and lung compliance. Static measurement of respiratory mechanics relies on end-inspiratory and end-expiratory occlusions, whereas dynamic measurement uses the least squares fitting method to assess compliance and resistance continuously during mechanical ventilation with no occlusion required (Brunner JX, Langenstein H, Wolff G. A simple method for estimating compliance. Crit Care Med. 1985;13(8):675-678. doi:10.1097/00003246-198508000-000141, Iotti GA, Braschi A, Brunner JX, et al. Respiratory mechanics by least squares fitting in mechanically ventilated patients: applications during paralysis and during pressure support ventilation. Intensive Care Med. 1995;21(5):406-413. doi:10.1007/BF017074092). Both methods can only be used in passive patients or in those patients with a minimal inspiratory effort, as the muscular part of a patient’s inspiratory effort can not be measured using airway pressure.

Compliance

Compliance (C) describes the elastic property of the respiratory system including the lung and the chest wall. Static compliance (C_STAT) is the ratio between a change in volume (V_T) and the corresponding change in transmural pressure (ΔP). The change in transmural pressure can be calculated as the difference between plateau pressure (P_PLAT) and total PEEP (PEEP_TOT) measured by an end-inspiratory and end-expiratory occlusion, respectively.

C_STAT = V_T/ΔP = V_T/ (P_PLAT - PEEP_TOT)

The dimension of compliance is usually ml/cmH2O. Elastance (E) is the reciprocal of static compliance.

E= ΔP/ V_T

Static compliance can be measured dynamically and continuously using the least squares fitting method (LSF) (Brunner JX, Langenstein H, Wolff G. A simple method for estimating compliance. Crit Care Med. 1985;13(8):675-678. doi:10.1097/00003246-198508000-000141, Iotti GA, Braschi A, Brunner JX, et al. Respiratory mechanics by least squares fitting in mechanically ventilated patients: applications during paralysis and during pressure support ventilation. Intensive Care Med. 1995;21(5):406-413. doi:10.1007/BF017074092). LSF estimates of static compliance are normally slightly lower than estimates obtained using the occlusion method.

In patients with a normal lung undergoing mechanical ventilation, C_STATis 50–60 ml/cmH2O (Arnal JM, Garnero A, Saoli M, Chatburn RL. Parameters for Simulation of Adult Subjects During Mechanical Ventilation. Respir Care. 2018;63(2):158-168. doi:10.4187/respcare.057753). Decreased compliance may occur in the case of ARDS, atelectasis, pneumothorax, lung fibrosis, or chest-wall stiffness. ARDS patients typically have a C_STAT of around 35–45 ml/cmH2O on admission (Table 1). C_STATdecreases with ARDS severity; therefore, monitoring compliance in ARDS patients can provide information about the volume of the aerated lung (baby lung concept).

An increase in compliance occurs in the case of lung emphysema.

Resistance

Resistance (R) describes the opposition to a gas flow entering the respiratory system during inspiration, which is caused by frictional forces. Resistance is calculated as the ratio between the pressure driving a given flow and the resulting flow rate (V̇).

R = ΔP / V̇

The dimension of resistance is usually cmH2O/(l/s).

The resistance of the respiratory system is primarily made up of the resistance of the airways and the endotracheal tube, because the resistance of the lung tissue is low.

Resistance can only be calculated in volume-control mode with a constant flow rate during inspiration.

R_INSP = (P_PEAK – P_PLAT)/ V̇_INSP

However, resistance is usually measured continuously using the least squares fitting method, which allows for differentiation between inspiratory and expiratory resistance. It is normal that the expiratory resistance is higher than the inspiratory resistance due to the shape of the airway tree, but a large discrepancy between inspiratory and expiratory resistance may suggest an expiratory flow limitation.

In mechanically ventilated patients with a normal lung and an artificial airway, inspiratory resistance (R_INSP) is 10–15 cmH2O/(l/s) (Arnal JM, Garnero A, Saoli M, Chatburn RL. Parameters for Simulation of Adult Subjects During Mechanical Ventilation. Respir Care. 2018;63(2):158-168. doi:10.4187/respcare.057753). A narrow endotracheal tube or use of a heat and moisture exchanger (HME) may cause an increase in R_INSP, which increases with flow in an exponential relationship (Gerbeaux P, Gainnier M, Arnal JM, Papazian L, Jean P, Sainty JM. Effects of helium-oxygen mixtures on endotracheal tubes: an in vitro study. J Biomech. 2005;38(1):33-37. doi:10.1016/j.jbiomech.2004.03.0194). Incorrect positioning or kinking of the endotracheal tube may also increase R_INSP. Increased airway resistance occurs in the case of COPD or asthma (Table 1).

Time constant

The time constant (RC) describes the speed of the change in volume after a step change in pressure and can be measured at both inspiration and expiration. The dimension is time expressed in seconds.

Due to the fact that a step change in pressure is associated with a change of volume according to an exponential curve, the exponential function indicates that it takes 1, 2, and 3 time constants to change the volume by 63%, 86%, and 95% of the total volume change.

Assuming a monocompartmental lung model, RC is the product of compliance and resistance measured at inspiration or expiration.

C_INSP= C_STAT x R_INSP

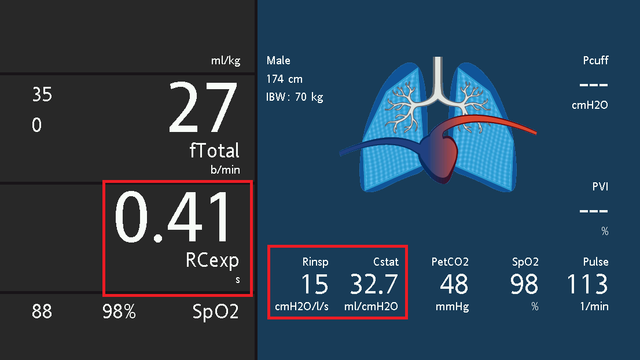
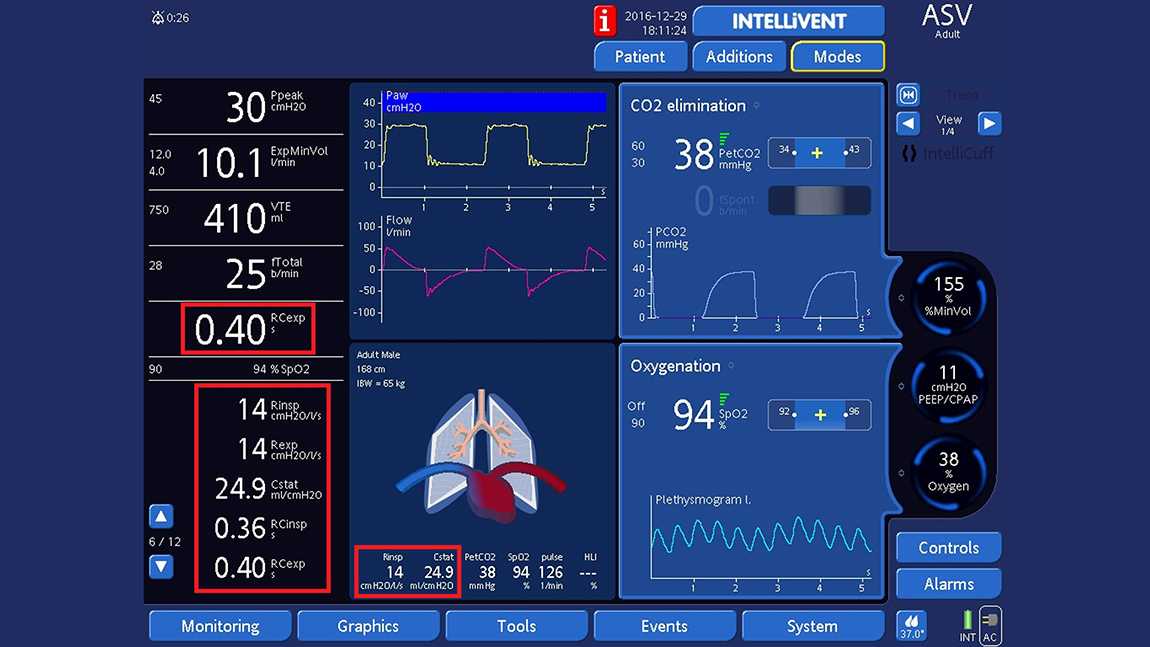
RC_EXP = C_STAT x R_EXP

As obstructive-disease patients have bicompartmental expiration mainly due to an expiratory flow limitation, measuring RC_EXP at 75% of the expired tidal volume will provide a more accurate result for the time constant of the slow compartment (Brunner JX, Laubscher TP, Banner MJ, Iotti G, Braschi A. Simple method to measure total expiratory time constant based on the passive expiratory flow-volume curve. Crit Care Med. 1995;23(6):1117-1122. doi:10.1097/00003246-199506000-000195, Lourens MS, van den Berg B, Aerts JG, Verbraak AF, Hoogsteden HC, Bogaard JM. Expiratory time constants in mechanically ventilated patients with and without COPD. Intensive Care Med. 2000;26(11):1612-1618. doi:10.1007/s0013400006326).

Its dependence on C and R means that RC_EXPis very useful for assessing the overall respiratory mechanics and the changes in them. The measurement is accurate in both passive and spontaneously breathing patients, assuming there is passive expiration. It can also be measured during noninvasive ventilation, provided there are no unintentional leaks.

Typical values for RC_EXP in mechanically ventilated patients with a normal lung are 0.5–0.7 s. A short time constant indicates a decrease in compliance, while a long time constant occurs in the case of increased resistance. A mixed condition with a decrease in compliance and an increase in resistance can result in a pseudo-normal RC_EXP.

Table 1: Typical values for respiratory mechanics in adult ICU patients intubated and passively mechanically ventilated

	Normal lungs	ARDS	COPD
Compliance (ml/cmH2O)	50–60	35–45	50–70
Resistance (cmH2O.s/l)	10–15	10–15	15–30
Expiratory time constant (s)	0.5–0.7	0.4–0.6	0.7–2.1

Expiratory time constant on Hamilton Medical ventilators

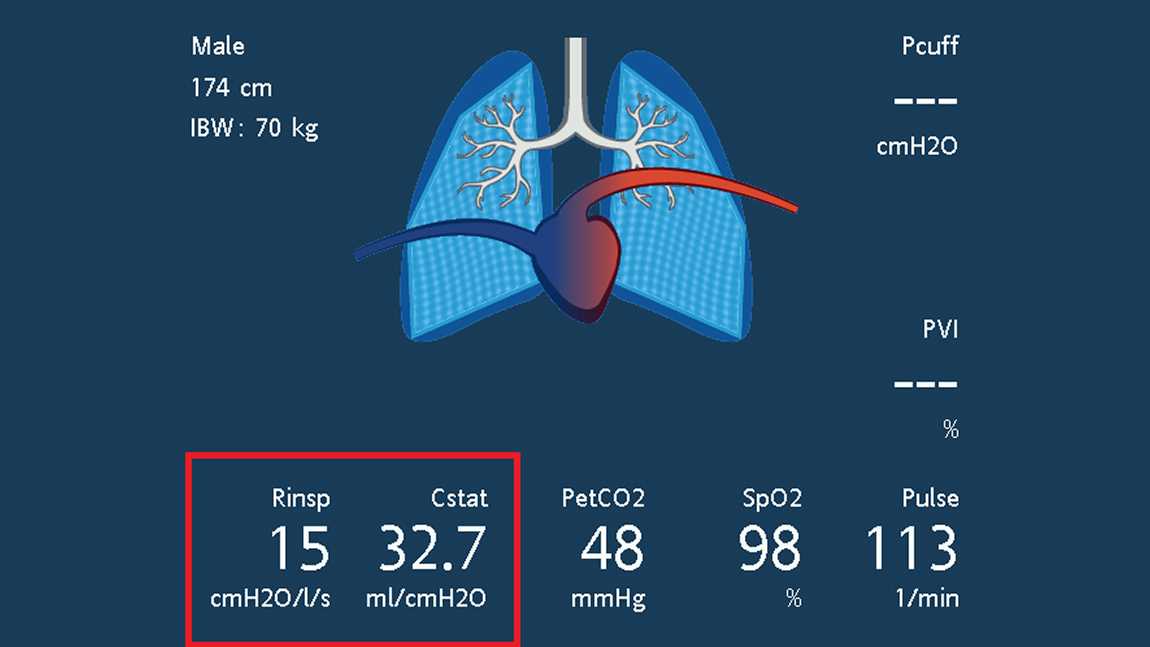
Hamilton Medical ventilators measure the RC_EXP breath-by-breath at 75% of the expiratory volume and use the least squares fitting method to continuously calculate compliance, as well as inspiratory and expiratory resistance. Results are shown on the monitoring panel and the Dynamic Lung (see Figs 1 and 2), and trends for all variables of respiratory mechanics can be displayed. In addition, clinicians can make their own measurements of C_STAT and R_EXPusing the occlusion method.

Screenshot showing dynamic lung, monitoring parameters, and oxygenation and ventilation windows

Screenshot showing dynamic lung and values for Rinsp, Cstat, and RCexp

Footnotes

References

1. Brunner JX, Langenstein H, Wolff G. A simple method for estimating compliance. Crit Care Med. 1985;13(8):675-678. doi:10.1097/00003246-198508000-00014
2. Iotti GA, Braschi A, Brunner JX, et al. Respiratory mechanics by least squares fitting in mechanically ventilated patients: applications during paralysis and during pressure support ventilation. Intensive Care Med. 1995;21(5):406-413. doi:10.1007/BF01707409
3. Arnal JM, Garnero A, Saoli M, Chatburn RL. Parameters for Simulation of Adult Subjects During Mechanical Ventilation. Respir Care. 2018;63(2):158-168. doi:10.4187/respcare.05775
4. Gerbeaux P, Gainnier M, Arnal JM, Papazian L, Jean P, Sainty JM. Effects of helium-oxygen mixtures on endotracheal tubes: an in vitro study. J Biomech. 2005;38(1):33-37. doi:10.1016/j.jbiomech.2004.03.019
5. Brunner JX, Laubscher TP, Banner MJ, Iotti G, Braschi A. Simple method to measure total expiratory time constant based on the passive expiratory flow-volume curve. Crit Care Med. 1995;23(6):1117-1122. doi:10.1097/00003246-199506000-00019
6. Lourens MS, van den Berg B, Aerts JG, Verbraak AF, Hoogsteden HC, Bogaard JM. Expiratory time constants in mechanically ventilated patients with and without COPD. Intensive Care Med. 2000;26(11):1612-1618. doi:10.1007/s001340000632

A simple method for estimating compliance.

Brunner JX, Langenstein H, Wolff G. A simple method for estimating compliance. Crit Care Med. 1985;13(8):675-678. doi:10.1097/00003246-198508000-00014

In intensive care medicine, pulmonary compliance is one of the very helpful diagnostic indices. Because of technical difficulties, however, the measurement of pulmonary compliance is often reduced to a rough guess of the compliance of the total respiratory system. The technical problems can be overcome using a computer to solve the basic equations with the least-squares fit (LSF) method. Unfortunately, this method requires such a long calculation time that bedside breath-by-breath calculations are impracticable on small computers. A simple computer algorithm (mean-values method) was therefore developed and compared to the LSF method. Compliance values calculated by either procedure were practically identical in ventilated patients. However, by reducing computing time to 30% of the LSF method, our mean-values algorithm enabled real-time estimation of compliance breath-by-breath.

Respiratory mechanics by least squares fitting in mechanically ventilated patients: applications during paralysis and during pressure support ventilation.

Iotti GA, Braschi A, Brunner JX, et al. Respiratory mechanics by least squares fitting in mechanically ventilated patients: applications during paralysis and during pressure support ventilation. Intensive Care Med. 1995;21(5):406-413. doi:10.1007/BF01707409

Link to article

OBJECTIVE

To evaluate a least squares fitting technique for the purpose of measuring total respiratory compliance (Crs) and resistance (Rrs) in patients submitted to partial ventilatory support, without the need for esophageal pressure measurement.

DESIGN

Prospective, randomized study.

SETTING

A general ICU of a University Hospital.

PATIENTS

11 patients in acute respiratory failure, intubated and assisted by pressure support ventilation (PSV).

INTERVENTIONS

Patients were ventilated at 4 different levels of pressure support. At the end of the study, they were paralyzed for diagnostic reasons and submitted to volume controlled ventilation (CMV).

MEASUREMENTS AND RESULTS

A least squares fitting (LSF) method was applied to measure Crs and Rrs at different levels of pressure support as well as in CMV. Crs and Rrs calculated by the LSF method were compared to reference values which were obtained in PSV by measurement of esophageal pressure, and in CMV by the application of the constant flow, end-inspiratory occlusion method. Inspiratory activity was measured by P0.1. In CMV, Crs and Rrs measured by the LSF method are close to quasistatic compliance (-1.5 +/- 1.5 ml/cmH2O) and to the mean value of minimum and maximum end-inspiratory resistance (+0.9 +/- 2.5 cmH2O/(l/s)). Applied during PSV, the LSF method leads to gross underestimation of Rrs (-10.4 +/- 2.3 cmH2O/(l/s)) and overestimation of Crs (+35.2 +/- 33 ml/cmH2O) whenever the set pressure support level is low and the activity of the respiratory muscles is high (P0.1 was 4.6 +/- 3.1 cmH2O). However, satisfactory estimations of Crs and Rrs by the LSF method were obtained at increased pressure support levels, resulting in a mean error of -0.4 +/- 6 ml/cmH2O and -2.8 +/- 1.5 cmH2O/(l/s), respectively. This condition was coincident with a P0.1 of 1.6 +/- 0.7 cmH2O.

CONCLUSION

The LSF method allows non-invasive evaluation of respiratory mechanics during PSV, provided that a near-relaxation condition is obtained by means of an adequately increased pressure support level. The measurement of P0.1 may be helpful for titrating the pressure support in order to obtain the condition of near-relaxation.

Parameters for Simulation of Adult Subjects During Mechanical Ventilation.

Arnal JM, Garnero A, Saoli M, Chatburn RL. Parameters for Simulation of Adult Subjects During Mechanical Ventilation. Respir Care. 2018;63(2):158-168. doi:10.4187/respcare.05775

Link to article

BACKGROUND

Simulation studies are often used to examine ventilator performance. However, there are no standards for selecting simulation parameters. This study collected data in passively-ventilated adult human subjects and summarized the results as a set of parameters that can be used for simulation studies of intubated, passive, adult subjects with normal lungs, COPD, or ARDS.

METHODS

Consecutive adult patients admitted to the ICU were included if they were deeply sedated and mechanically ventilated for <48 h without any spontaneous breathing activity. Subjects were classified as having normal lungs, COPD, or ARDS. Respiratory mechanics variables were collected once per subject. Static compliance was calculated as the ratio between tidal volume and driving pressure. Inspiratory resistance was measured by the least-squares fitting method. The expiratory time constant was estimated by the tidal volume/flow ratio.

RESULTS

Of the 359 subjects included, 138 were classified as having normal lungs, 181 as ARDS, and 40 as COPD. Median (interquartile range) static compliance was significantly lower in ARDS subjects as compared with normal lung and COPD subjects (39 [32-50] mL/cm H2O vs 54 [44-64] and 59 [43-75] mL/cm H2O, respectively, P < .001). Inspiratory resistance was significantly higher in COPD subjects as compared with normal lung and ARDS subjects (22 [16-33] cm H2O/L/s vs 13 [10-15] and 12 [9-14] cm H2O/L/s, respectively, P < .001). The expiratory time constant was significantly different for each lung condition (0.60 [0.51-0.71], 1.07 [0.68-2.14], and 0.46 [0.40-0.55] s for normal lung, COPD, and ARDS subjects, respectively, P < .001). In the subgroup of subjects with ARDS, there were no significant differences in respiratory mechanics variables among mild, moderate, and severe ARDS.

CONCLUSIONS

This study provides educators, researchers, and manufacturers with a standard set of practical parameters for simulating the respiratory system's mechanical properties in passive conditions.

Effects of helium-oxygen mixtures on endotracheal tubes: an in vitro study.

Gerbeaux P, Gainnier M, Arnal JM, Papazian L, Jean P, Sainty JM. Effects of helium-oxygen mixtures on endotracheal tubes: an in vitro study. J Biomech. 2005;38(1):33-37. doi:10.1016/j.jbiomech.2004.03.019

QUESTION

To determine flow pattern and critical Reynolds numbers in endotracheal tubes submitted to different helium-oxygen mixtures under laboratory conditions.

MATERIALS AND METHODS

Flow-pressure relationships were performed for seven endotracheal tubes (rectilinear position, entry length applied) with distal end open to atmosphere (predicted internal diameters: 6-9 mm). Nine helium-oxygen mixtures were tested, with FIHe varying from zero to 0.78 (increment: 10%). Nine flows were tested, with rates varying from 0.25 to 1.60 l s(-1) (increment: 0.15 l s(-1)). Gas flow resistance was calculated, and for each endotracheal tube, a Moody diagram was realised. Flow regime and critical Reynolds numbers were then determined (fully established laminar, nonestablished laminar, smooth turbulent, or rough).

RESULTS

Even low concentration of helium in inspiratory mixture reduces endotracheal tubes resistance. Effect is maximal for high flows, small tube and high FIHe. Critical Reynolds numbers are inversely correlated to tube diameter.

ANSWER

Under laboratory conditions, flow pattern in endotracheal tubes varies from fully established laminar to rough. Knowledge of the critical Reynolds numbers allows correct application of fluid mechanic formula when studying tube or gaseous mixture effects on respiratory mechanisms.

Simple method to measure total expiratory time constant based on the passive expiratory flow-volume curve.

Brunner JX, Laubscher TP, Banner MJ, Iotti G, Braschi A. Simple method to measure total expiratory time constant based on the passive expiratory flow-volume curve. Crit Care Med. 1995;23(6):1117-1122. doi:10.1097/00003246-199506000-00019

Link to article

OBJECTIVE

In intubated, mechanically ventilated patients, inspiration is forced by externally applied positive pressure. In contrast, exhalation is passive and depends on the time constant of the total respiratory system. The expiratory time constant is thus an important determinant of mechanical ventilation. The aim of this study was to evaluate a simple method for measuring the expiratory time constant in ventilated subjects.

DESIGN

Prospective study using a lung simulator and ten dogs.

SETTING

University hospital.

SUBJECTS

Commercially available lung simulator and ten greyhound dogs.

INTERVENTIONS

Different expiratory time constants were set on the lung simulator. In the dogs, the endotracheal tube was clamped to increase airways resistance by 22.5 cm H2O/(L/sec) and the lungs were injured with hydrochloric acid to decrease total respiratory compliance by 16 mL/cm H2O. This procedure resulted in a wide range of expiratory time constants.

MEASUREMENTS AND MAIN RESULTS

Pneumotachography was used to measure flow and volume. The ratio of exhaled volume and peak flow was calculated from these signals, corrected for the limited exhalation time yielding the "calculated expiratory time constant" and compared with the actual expiratory time constant. The typical error was +/- 0.19 sec for the lung simulator and +/- 0.15 sec for the dogs.

CONCLUSIONS

The volume and peak flow corrected for limited exhalation time is a good estimate of the total expiratory time constant in passive subjects and may be useful for the titration of mechanical ventilation.

Expiratory time constants in mechanically ventilated patients with and without COPD.

Lourens MS, van den Berg B, Aerts JG, Verbraak AF, Hoogsteden HC, Bogaard JM. Expiratory time constants in mechanically ventilated patients with and without COPD. Intensive Care Med. 2000;26(11):1612-1618. doi:10.1007/s001340000632

Link to article

OBJECTIVE

In mechanically ventilated patients, the expiratory time constant provides information about the respiratory mechanics and the actual time needed for complete expiration. As an easy method to determine the time constant, the ratio of exhaled tidal volume to peak expiratory flow has been proposed. This assumes a single compartment model for the whole expiration. Since the latter has to be questioned in patients with chronic obstructive pulmonary disease (COPD), we compared time constants calculated from various parts of expiration and related these to time constants assessed with the interrupter method.

DESIGN

Prospective study.

SETTING

A medical intensive care unit in a university hospital.

PATIENTS

Thirty-eight patients (18 severe COPD, eight mild COPD, 12 other pathologies) were studied during mechanical ventilation under sedation and paralysis.

MEASUREMENTS AND RESULTS

Time constants determined from flow-volume curves at 100%, the last 75, 50, and 25% of expired tidal volume, were compared to time constants obtained from interrupter measurements. Furthermore, the time constants were related to the actual time needed for complete expiration and to the patient's pulmonary condition. The time constant determined from the last 75% of the expiratory flow-volume curve (RCfv75) was in closest agreement with the time constant obtained from the interrupter measurement, gave an accurate estimation of the actual time needed for complete expiration, and was discriminative for the severity of COPD.

CONCLUSIONS

In mechanically ventilated patients with and without COPD, a time constant can well be calculated from the expiratory flow-volume curve for the last 75% of tidal volume, gives a good estimation of respiratory mechanics, and is easy to obtain at the bedside.